Z-score and Probability
Strictly speaking, a z-score (almost always named a regular score) represents the fundamental building block of just how far a piece of data would be from the average. But more theoretically, it's a calculation of how many normal deviations mean a raw score is below or above the population.
It is appropriate to incorporate a z-score on a standard normal distribution. Z-scores range between -3 standard deviation ( sd ) to +3 standard deviations (which would also fall to something like the extreme left of the standard normal distribution) (which would fall to the far right of the normal distribution curve). (which would fall to the far right of the normal distribution curve). (which would fall to the far right of the normal distribution curve). You need to know the mean μ and also the population standard deviation σ to use a z-score.
A new production and distribution and one that has a mean of zero and a standard deviation of one are developed and implemented by translating a distribution of observations into z-scores. This already has many applications, but the primary one is that it enables us to start mapping observed ratings to the values of likelihood.
If sometimes you find the Z-score also for a value i.e. standardize the value) for every standard normal distribution, the probability distribution is converted into a standard normal and you can use the normally distributed information to find probability distribution.
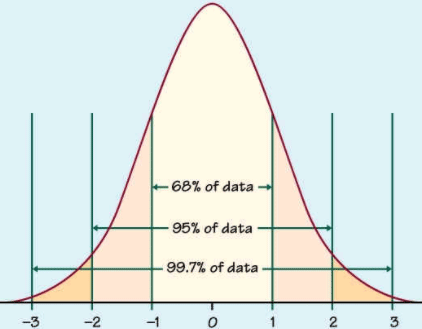
Let's assume that means, for example in this case, that U.S. adult heights and weights are all normally distributed. They will have distinct means and standard deviations. However, you could find your z-score for your weight and height if you knew these means and standard deviations.
In order to find the likelihood, say, of a randomly selected U.S. adult weighing less than you or taller than you, you can now use the Regular Normal Table.
With care in the first place, the Z-score can and should be accurately measured and interpreted differently. The Z-score is not prone to false accounting methods, for instance. The Z-score would be just as reliable as the information that goes into it because business organizations in trouble can often distort or cover up certain financials.
Consequently, for local enterprises with hardly any to zero revenues, the Z-score is not very accurate. Those same organizations would score low regardless of their actual financial health. In addition, the Z-score doesn't answer a company's cash flows. Rather, with the use of the networking capital-to-asset ratio, it just points to it.
Ultimately, if a company reports one-time write-offs, Z-scores will swing from quarter to quarter. Such incidents can modify the final score and can wrongly imply that a business is on the verge of bankruptcy.